MO405 - Questão para a prova oral
Número: 039
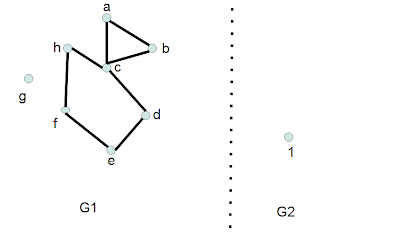
Enunciado: Considere o Grafo G resultante da diferença simétrica de G1 e G2, e assinale a alternativa correta:
I. G possui um ciclo de tamanho 5;
II. G possui um caminho maximal de tamanho 3;
III.O tamanho da menor cobertura por vértices de G é 3.
II. G possui um caminho maximal de tamanho 3;
III.O tamanho da menor cobertura por vértices de G é 3.
a) Somente I está correta;
b) Somente II está correta;
c) I e II estão corretas;
d) I e III estão corretas;
e) N.D.A